Das ideale Kraftwerk - oder:
Carnot-Kreisprozess

(Ein Beitrag aus der Reihe "Hintergründe").

 Dr. Wolfgang Feist leitet das Passivhaus-Institut in Darmstadt. Er ist Dipl.-Physiker und promovierter Bauphysiker. 

Wärme ist eine Energieform - allerdings handelt es sich um Energie, die in statistischer Weise verteilt ist und die sich nicht in beliebigem Umfang in hochwertige Arbeit umwandeln lässt. (Vgl. unsere Seite zum Thema "Zweiter Hauptsatz der Thermodynamik").

Eine Maschine, die Wärme(-energie) in mechanische Arbeit umwandelt nennen wir ein Wärmekraftwerk oder eine Wärmekraftmaschine. Diese Maschinen spielen in der Praxis eine große Rolle - aber auch in der physikalischen Thermodynamik.

Im Beitrag zum Zweiten Hauptsatz haben wir bewiesen, dass ein Kraftwerk immer nur einen Teil der Wärme, die es zur Verfügung gestellt bekommt, in Arbeit umwandeln kann - einen gewisser "Tribut" der Wärme muss an ein zweites untere Temperaturreservoir abgegeben werden. Die Obergrenze des Wirkungsgrades hängt nur von den Temperaturen To und Tu der verfügbaren Reservoire ab; erreicht wird genau dieser Grenzwirkungsgrad, wenn eine reversibel arbeitende Wärmekraftmaschine verwendet wird.(reversibel = zeitumkehrbar, der Prozess kann auch rückwärts laufen)


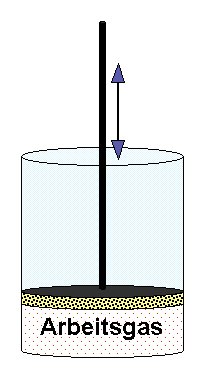ideales Gas mit spez. Wärmekapazität cV und der Masse m.


Nicolas Léonard Sadi Carnot hat schon 1824 in Gedanken eine Maschine entworfen, die prinzipiell in der Lage ist, zwischen den Temperaturen To und Tu reversibel zu arbeiten:

Die Carnot-Maschine benutzt ein ideales Gas als Arbeitsmedium. Es wird in einem Zylinder, der durch einen freigängigen und wärmegedämmten Arbeitskolben gasdicht abgeschlossen ist, eingesetzt (Bild links). Der Kolben ist reibungsfrei beweglich; an der Kolbenstange kann Arbeit abgenommen oder zugeführt werden.

Dieses Arbeitssystem kann z.B. thermisch ideal isoliert werden, in dem es in eine isoliernde Hülle gestellt wird (Wärmedurchgang = 0, im Folgenden "hellgelb" gezeichnet) .

Das Arbeitssystem wird ergänzt durch zwei Temperaturreservoire: Ein "heißes Reservoir" (rot) mit der unter allen Umständen konstanten Temperatur To und ein "kühles Reservoir" mit der unter allen Umständen konstanten Temperatur Tu (blau). Die Reservoire können jeweils bei ihrer Tempeartur Wärme aufnehmen bzw. abgegeben, ohne dass die Temperatur sich ändert (es sind ideale Wärmequllen bzw. Wärmesenken). Die Reservoire haben eine Form, die es erlaubt, den Arbeitszylinder in vollflächingen idealen thermischen Kontakt zu bringen ("quasis-unendlicher Wärmeübergangskoeffizient"). Dadurch kann Wärme ohne nennenswerte Temperaturdifferenz zwischen dem Arbeitsgas im Zylinder und den Reservoiren übertragen werden.

Wir lassen das Maschinchen erst einmal laufen (siehe links), in dem wir es vom komprimierten Zustand aus erst einmal im Kontakt mit der heißen Wärmequelle arbeiten lassen (bei Hitze kommt da was rüber), es dann isolieren und so lang weiterarbeiten lassen, bis es abkühlt ist (auf Tu), dann in Kontakt mit dem kalten Reservoir bringen und in der Kälte (mit wenig Aufwand) erneut komprimieren und schließlich ganz zum Schluß etwas Arbeit aufbringen, um noch weiter so lange isoliert zu komprimieren, bis die Temperatur To wieder erreicht wird. Das Spielchen kann beliebig wiederholt werden, deswegen nennt man den Carnot-Prozess auch einen Kreisprozess.

Übrigens: Fachleute reden für den Ablauf bei "isolierten" Prozesschritten auch von "adiabat", bei Abläufen mit konstanter Temperatur von "isotherm".

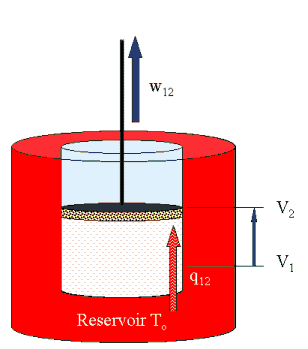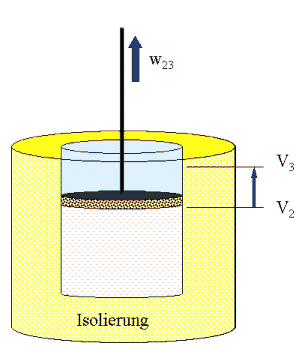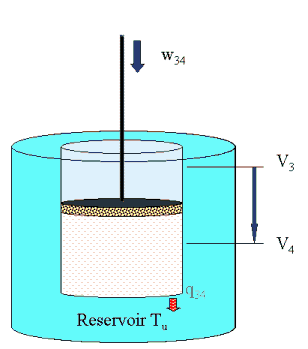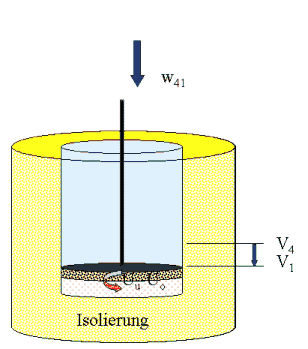
(I)     1 → 2 isotherm bei To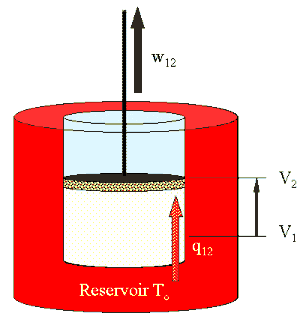
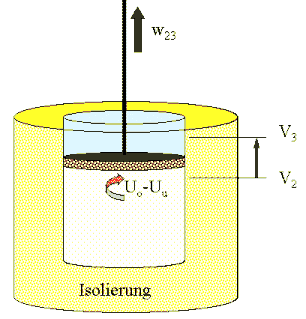
(II)    2→ 3 isoliert (adiabat)

Es besteht Kontakt zum heißen Reservoir
(rot: Wärmequelle bei To ).
Das Arbeitsgas dehnt sich bei konstanter Temperatur von V1 auf V2 aus und leistet dabei die Arbeit w12. Die Energie dafür entnimmt die Maschine aus dem Reservoir der Temperatur To als Wärme: q12 = w12.

Diese Arbeit wird hier ausgerechnet, das Ergebnis ist:

w12 = m R To ln (V2/V1 )

 

 

 

 

 

Jetzt wird das Gas isoliert: Es gibt keinen Wärmeaustausch mit der Umgebung (gelb = idealer Dämmstoff). Wir lassen aber zu, dass sich das Gas weiter ausdehnt (das macht es, wenn es darn nicht gehindert wird). Die Arbeit, die es dabei weiter leisten kann, w23, nehmen wir an der Kolbenstange ab. Beim Ausdehnen kühlt sich das isolierte Gas ab - es entnimmt die geleistetet Arbeit aus der Inneren Energie (Wärmebewegung) der Gasmoleküle. Wir lassen das solange zu, bis die Temperatur gleich Tu ist. Da ist das Volumen V3. Es gilt nach dem Energiesatz

w23 = mcV ( To - Tu )

 

 
(III)    3→ 4 isotherm bei Tu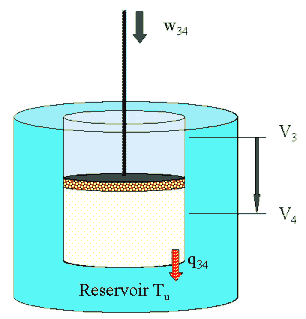
(IV)    4→ 1isoliert (adiabat)

Es besteht Kontakt zum kalten Reservoir
(blau: Wärmesenke bei Tu).
Das Arbeitsgas wird von außen über die Kolbenstange bei konstanter Temperatur von V3 auf V4 komprimiert und dazu die Arbeit w34 aufgewendet. Die Energie gibt die Maschine über das Gas an das Reservoir der Temperatur Tu als Wärme ab: q34 = w34. Das ist der Obulus, der an Wärme "gezahlt" werden muss, um die Maschine am Laufen zu halten. Wir zahlen diesen Obulus bei einer niedrigen Temperatur; er ist umso kleiner, je niedriger die Tempertur Tu ist, die zur Verfügung steht. Wie oben berechnet sich die aufzubringende Arbeit zu

w34 = m ·R ·Tu ln ( V3 / V4).

(vgl. Rechengang).

 

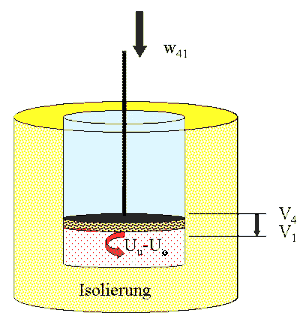
Noch einmal wird das Gas isoliert: Es gibt keinen Wärmeaustausch mit der Umgebung (gelb = idealer Dämmstoff). Wir komprimieren das Gas unter Arbeistaufwand weiter. Die Arbeit, die es dazu braucht, w41, führen wir an der Kolbenstange zu. Beim Komprimieren erhitzt sich das isolierte Gas - die Innere Energie (Wärmebewegung) der Gasmoleküle steigt. Wir komprimieren so lange, bis die Temperatur gleich To ist. Da ist das Volumen V1 und wir sind wieder beim Anfangszustand. Es gilt nach dem Energiesatz

w41 = mcV ( Tu - To )

Das ist übrigens gerade die Arbeit, die in Phase II freigesetzt wurde. Die Arbeistbilanz der Phasen (II) und (IV) zusammen ist Null. Die Wärmebilanz ist wegen der Isolierung ohnehin Null.

Mit der hier beschriebenen Carnot-Maschine haben wir ein prinzipiell auch in umgekehrter Richtung arbeitendes Kraftwerk. Die Carnot-Maschine ist also ein reversibles Kraftwerk - aus dem Zweiten Hauptsatz folgt, dass die Carnot-Maschine damit den maximalen thermodynamischen Wirkungsgrad bei der Umwandlung von Wärme aus dem Temperaturreservoir To mit Abwärmeabgabe an das Reservoir Tu hat. Damit wird die Bedeutung dieses Gedankenexperimentes klar: Es liefert sozusagen die Kalibrierung der Thermodynamik.

In der Praxis lässt sich eine Maschine, die den Carnot-Prozess verwenden soll, nur umständlich realisieren. Einfacher zu bauen ist die sogenannte "Stirling-Maschine". Auch der Stirling-Kreisprozess ist ein reversibel arbeitendes Kraftwerk - und er hat daher den gleichen Wirkungsgrad wie eine Carnot-Maschine. Modelle, die nach dem Stirling-Kreisprozess arbeiten, sind sogar am Markt zu erhalten. Sie eignen sich sehr gut für die Demonstration von thermodynamischen Grundlagen in der Schule.

Ein "Kraftwerk" kann aus Wärme Q, die einem Reservoir der Temperatur To entnommen wird, nur dann nutzbare Arbeit gewinnen, wenn es zugleich auch einen Teil der Wärme an ein zweites Reservoir mit niedrigerer Temperatur Tu (häufig wird die "Umgebung" verwendet) abgeben kann. Die maximal gewinnbare Arbeit W aus der dem oberen Reservoir entnommenen Wärme beträgt η Carnot ⋅ Q. Dabei ist η Carnot der sogenannte Carnot-Wirkungsgrad:

.

Ein Kraftwerk ist eine Maschine, deren Zweck darin besteht, Wärme in Arbeit umzuwandeln und die sich dazu einer Wärmequelle bedient.

Ein Reservoir ist ein thermodynamisches Gleichgewichtssystem, das seinen Zustand konstanter Temperatur auch bei Entnahme und Zufuhr von Wärme beibehält.

Carnot ist ein berühmter französischer Physiker. Er war einer der Ersten, welcher die hier beschriebenen Zusammenhänge aufgeklärt hat.


Schlussbemerkung:

Manche Abhandlungen im Internet, gerade auch solche von "führenden Professoren", erwecken den Eindruck, als ob

  1. Die Grundlagen der Thermodynamik nur von Spezialisten verstanden werden könnten; alle anderen Personen sollten sich doch bitte heraushalten - das unterstreicht sich am besten dadurch, dass auch einfachste Zusammenhänge in nicht erklärtem "Fachinesisch" formuliert werden. Und dass insbesondere ständig auf formalen Begrifflichkeiten herumgeriten wird. Einzig anschaulich wird es dann, wenn wieder einmal gefordert wird, doch bitte nicht "Äpfel mit Birnen" zu vergleichen. De Abhandlungen bestehen denn auch überwiegend aus etwas herablassend formulierten Aufklärungen darüber, "... was alles nicht geht, im Gegensatz zu den naiven Vorstellungen mancher (dummer) Öko-Ideologen." Ich will hier nicht in Abrede stellen, dass es auch Verbohrte bei den ökologisch verantwortlich denkenden Menschen gibt. Indes legt der Ideologievorwurf, erhoben von einem Interessenvertreter, immer nahe, einmal den von ihm vertretenen Wahrheitsanspruch auf Vorurteile zu prüfen. Gerade bei den negativen Attributen, die jemand bei anderen gehäuft zu erkennen glaubt, liegt ganz oft sein eigenes Problem,. Übrigens: Ideologiefreiheit gibt es nicht - die Naturwissenschaft spricht in diesem Zusammenhang bevorzugt von Paradigmen oder Theoriegebäuden.
  2. Die heutigen technischen Realisationen von Maschinen bei der Energieumwandlung "an die Grenzen des thermodynamisch Machbaren" gehen - sprich, höchstmöglich effizient sind und vernünftigerweise keine (entscheidenden) Verbesserungen erlauben. Wozugibt es sonst die vielen gut bezahlten Fachleute? In weiteren Internet-Seiten dieser Reihe wird allgemein verständlich dargestellt, wie gut wir heute tatsächlich sind - und warum wir immer noch sehr viel besser werden können. Die Frage, warum wir dann nicht alles tun, um noch besser zu werden, wird hier nicht behandelt, das ist keine technische und auch keine naturwissenschaftliche Frage.

 

In loser Folge werden weitere Beiträge in der Reihe "Hintergründe" erscheinen.

Bereits erschienene Artikel:

Der Zweite Hauptsatz der Thermodynamik

Ein wenig Strahlungsphysik

Apsorption und Emission - ein auf den ersten Blick überraschender Zusammenhang

Wärmespeichern oder Wärmedämmen

 

 

Berechnung der Arbeit, die ein ideales Gas bei isothermer Ausdehnung leistet

Das geht leider nicht ohne ein wenig Mathematik - sorry. Wem das zu anstrengend ist oder zu "fachchinesisch", braucht es nicht zu verstehen. Das Ergebnis steht schon oben und es wird von Niemandem (ernsthaft) bezweifelt.

Arbeit ist Kraft mal Weg, die Kraft ergibt sich aus dem Druck p des Gases auf den Kolben mal dem Kolbenquerschnitt (das ist der Querschnitt A des Zylinders, Innenmaß). Bewegt sich der Kolben um ein kleines Stück "ds", dann nimmt das Gasvolumen V um dV mit

dV = A · ds

zu. Die auf dem Wegstückchen ds geleistete Arbeit ist

dw = p · A · ds = p · dV .

Führen wir die ganze Ausdehnung von V1 bis V2 in kleinen Einzelstückchen durch, so kann die gesamte gewonnnene Arbeit als Summe (in der Verfeinerung "Integral")

w12 = ∫ p dV          zwischen den Zuständen V1 und V2

geschrieben werden. Es ist nach der Gasgleichung

p ·V = m ·R · To

somit lässt sich der Druck als Funktion des Volumens bestimmen:

p = m ·R ·To· V-1

Das wieder eingesetzt in das "Integral" gibt

w12 = ∫ m ·R ·To· V-1 dV             zwischen den Zuständen V1 und V2

m ·R und To sind konstant und können vorgezogen werden. Es bleibt das Integral über x-1 dx, Sie erinnern sich, das war ein wenig sonderbar - die Stammfunktion ist der Logarithmus ln(x):

w12 = m ·R ·To ln ( V2 / V1 ).

 

Ganz analog zum obigen Rechengang ergibt sich für den Prozessschritt (III)

w34 = m ·R ·Tu ln ( V3 / V4).

Bitte bedenken, das hier nun die Temperatur Tu vorliegt. Aus ein wenig Rechnerei mit der Gasgleichung folgt übrigens V2/V1 = V3/V4 für den Carnot-Kreisprozess.

Link zu Informationen zum Passivhaus: Passivhaus-Grundlagen.

Link zur Homepage der Passivhaustagung: Passiv Haus Konferenz.

Link zur Homepage des Passivhaus Institutes:

(aktualisiert 25.05.2007 Autor: Dr. Wolfgang Feist 
 © Passivhaus Institut; unveränderte und ungekürzte Wiedergabe unter Angabe der Quelle gestattet. Diese Seiten werden ständig aktualisiert und erweitert.)